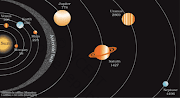
The Ptolemaic Model
“The Ptolemaic model accounted for the apparent motions of the planets in a very direct way, by assuming that each planet moved on a small sphere or circle, called an epicycle, that moved on a larger sphere or circle, called a deferent. The stars, it was assumed, moved on a celestial sphere around the outside of the planetary spheres”. See figure
"Ptolemy’s Model The basic features, drawn roughly to scale, of the geocentric model of the inner solar system that enjoyed widespread popularity prior to the Renaissance. The planets’ deferents were considered to move on spheres lying within the celestial sphere that held the stars. The celestial sphere carried all interior spheres around with it, but the planetary (and solar) spheres had additional motions of their own, causing the Sun and planets to move relative to the stars. To avoid confusion, partial paths (dashed) of only two planets, Venus and Jupiter, are drawn here".
Copernicus Model
"In the early 1500s, when virtually everyone believed Earth was the center of the universe, Polish scientist Nicolaus Copernicus proposed that the planets instead revolved around the sun. Although his model wasn't completely correct, it formed a strong foundation for future scientists to build on and improve mankind's understanding of the motion of heavenly bodies". See figure
“The Copernican Planisphere, illustrated in 1661 by Andreas Cellarius. Credit: Public domain”.
Look at the planet orbit in the above image, the orbit is a circle that its center is on another circle.
Kepler's laws of planetary motion
The importance of Kepler's work was that for the first time, showed the planet's orbit is ellipse instead of circles.
Kepler’s First Law: Planets move in elliptical orbits with the Sun at one focus of the ellipse. See figure
Kepler’s second Law: A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. See figure
Kepler’s 3rd law: The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit. See figure
Earth-Sun Orbit
“The motion of the Earth around the Sun is a very important motion. Some early Greek philosophers initially decided that the earth was in orbit around the sun, but they could not solve the mathematics. Deciding that they could not make the arithmetic fit, they stated that the Sun revolved around the Earth.”
“The reason the arithmetic could not be solved is that the Earth is not rotating around the Sun. The Sun does not rotate around the Earth, and the Earth does not rotate around the sun. Neither theory was completely correct. Newton finally solved the problem around 1666. It required his understanding of gravity to realize that the Earth is not traveling around the Sun. The Earth and Sun act as a system. Imagine the Earth and Sun hooked together by a weightless strong rod. Where would it balance? Because the Sun is much heavier than the Earth, the system would balance near, but not at, the center of the Sun. The Earth and the Sun are traveling around a common center of mass, or the common center of gravity of the Earth-Sun system". See figure
“Center of the Earth-Sun system, around which the system revolves, is not at the center of mass of the Sun, although very close to it”.
“Gravity affects the orbit of the Earth by producing an orbit, which is not a circle. The orbit is slightly elongated into something more eccentric (termed an ellipse) than a perfect circle. At times the Earth is closer to the Sun that at others (Figure).”
Newton's gravitational force and Kepler’s laws
“How did Newton make use of Kepler’s laws to deduce the law of gravitational force? An important thing to understand first is why Newton was convinced that a mechanical explanation of planetary motion was needed. For Aristotle and even for Copernicus more than eighteen centuries later, circular motion was the “natural” motion in the heavens. It was the way stars or planets move when left to themselves”.
“Galileo was the first to state that undisturbed motion (“natural” motion) is motion in a straight line with constant velocity. This indeed sounds like Newton’s first law”.
“Newton’s imagination was able to cut loose from the bonds of earthly gravity that had held back Galileo. He unhesitatingly extended Galileo’s principle of inertial motion on to infinity and stated it as his first law of mechanics. This was a necessary first step to the discovery of the law of universal gravitation. If the “natural” motion of a planet in the absence of force is straight-line motion, the actual orbital motion requires an explanation. A force must be acting to deflect the planet from its otherwise straight course into its curved path around the Sun”.
"The idea of an inverse square law of gravitational force acting on the planets was in the air around Newton’s time. His genius lay not so much in thinking of it as in demonstrating its validity mathematically and weaving it into a coherent theory of universal gravitation. The really crucial test of the inverse square law is provided by Kepler’s first law, the statement that planets move in elliptical orbits with the Sun at one focus. In London in 1684, Edmund Halley, Robert Hooke, and Sir Christopher Wren worked at the problem of connecting the elliptical orbits of the planets to the law of force emanating from the Sun. Although they believed in the inverse square law, they failed to connect it to Kepler’s first law of elliptical motion."
Finally Halley journeyed up to Cambridge to ask Newton about the problem. Here is an account of their meeting written soon afterward by John Conduitt. “Without mentioning either his own speculations, or those of Hooke and Wren, he [Halley] at once indicated the object of the visit by asking Newton what would be the curve described by the planets on the supposition that gravity diminished as the square of the distance. Newton immediately answered, an Ellipse. Struck with joy and amazement, Halley asked him how he knew it? ‘Why,’ replied he, ‘I have calculated it.’ ” Three years later, in 1687, under the auspices of Halley, Newton’s monumental Principia was published".






0 Comments